Mathematik

Die Mathematik gibt Ihnen die Möglichkeit mathematische Operationen mit bis zu 20 Variablen durchzuführen. Die Variablen werden durch Eingangswerte bestimmt.

Inhalt

Ein- und Ausgänge

Eingänge

GATE (siehe Logikelemente | Datenpunkt-Gate)
IN 1–…
Jede Variable wird durch einen Eingang repräsentiert. Es sind maximal 20 Eingänge möglich.

Ausgänge

OUT
Das Ergebnis der Berechnung.

Konfiguration

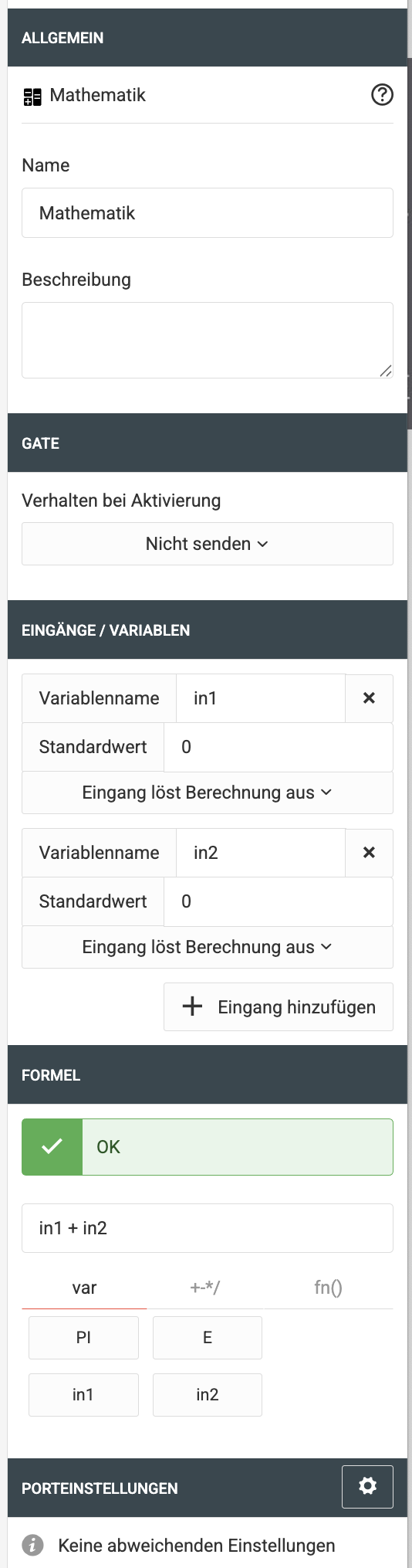
Eingänge

Es sind insgesamt 20 Eingänge möglich.

Bezeichnung

Sie können die zu den Eingängen korrespondierenden Variablenbezeichnungen anpassen. Standardmäßig werden die Variablen mit in1, in2, …, in20 benannt.
Hinweis: Leerzeichen in der Bezeichnung führen zu Fehlern bei der Ausführung der Formel.

Standardwert

Sollte noch kein Wert am zugehörigen Eingang anliegen, oder der anliegende Wert nicht als Fließkommawert (Float) verwendet werden können, wird der hinterlegte Standardwert für die Berechnung verwendet.

Ausführung

Sie können hier festlegen, ob eine Berechnung ausgelöst werden soll, wenn am entsprechenden Eingang ein neuer Wert eingeht. Es ist an dieser Stelle noch nicht von Belang, ob dieser Wert später als Fließkommawert (Float) Verwendung finden kann.
Optionen sind:

Eingang löst Berechnung aus
Bei jedem Eingang wird eine Berechnung angestoßen
Eingang löst keine Berechnung aus
Es wird niemals eine Berechnung ausgelöst. Der Wert wird aber zur Berechnung verwendet.
Wertänderung löst Berechnung aus
Es wird nur dann eine Berechnung ausgelöst, wenn der sich der Wert des Eingangs ändert. Wird z.B. 100 mal hintereinander eine 1.0 gesendet, wird nur beim ersten Mal eine Berechnung ausgelöst.

Hinzufügen und Löschen

Über das Symbol + werden neue Eingänge hinzugefügt und über das werden einzelne Eingänge wieder entfernt.

Formel

In der Formel können Sie auf alle definierten Variablen zurückgreifen. Es gilt Punkt- vor Strichrechnung. Durch Klammerung kann die Berechnungsreihenfolge beeinflusst werden. Neben den durch Sie festgelegten Werten haben Sie folgende unterstützende Variablen und Funktionen zur Verfügung:

Variablen

Name	Beschreibung
pi	Die Kreiszahl – Genauigkeit etwa 3,141592653589793
e	Die Eulersche Zahl – Genauigkeit etwa 2,718281828459045

Operatoren

Name	Beschreibung
+	Addition
-	Subtraktion
*	Multiplikation
/	Division
**	Potenzierung
%	Modulo (Restwert)

Funktionen

Name	Parameter	Beschreibung
sin(x)	1	Sinus
cos(x)	1	Cosinus
tan(x)	1	Tangens
asin(x)	1	Arkussinus
acos(x)	1	Arkuskosinus
atan(x)	1	Arkustangens
abs(x)	1	Der absolute Wert der Übergabe - Aus -10.0 wird 10.0
ceil(x)	1	Aufrunden
floor(x)	1	Abrunden
log(x)	1	Logarithmus
sqrt(x)	1	Quadratwurzel
rand()	0	Zufallszahl zwischen 0.0 und 1.0
max(x,y)	2	Größter Wert
min(x,y)	2	Kleinster Wert

Der Dezimaltrenner ist der Punkt ".". Die Auswertung der Variablen und Funktionen beachtet die Groß-/Kleinschreibung. So entspricht pi nicht Pi oder PI oder pI.

Beispiele

rand() * 100.0
Erzeugt eine Zufallszahl von 0.0 bis 100.0
min(in1, in2)
Wobei in1 = 10.0 und in2 = 8.0 - Ergebnis wäre 8.0
2**2 - sqrt(4) - Ergibt 0 - 2² ergibt 4 und die Wurzel aus 16 ist auch vier. Die Subtraktion wird zuletzt ausgeführt
ceil(2.333)
Ergibt 3
floor(2.6)
Ergibt 2
floor(in1 + 0.5)
Wobei in1 = 2.6 - Ergibt 3. Auf diese Weise kann man kaufmännisch runden.

///