Mathematik
Der Mathematik-Job bietet nicht nur alle gängigen Mathematik Operationen, sondern darüber hinaus auch eine Menge mathematischen Funktionen. Am Ende dieser Beschreibung finden Sie ein paar Beispiele.
EIS-Formate
Der Mathematik Job unterstützt folgende Datentypen am Ein- und Ausgangsobjekt:
EIS 1 (1 Bit)
EIS 5 (2 Byte FP)
EIS 6 (1 Byte)
EIS 9 (4 Byte FP)
EIS 10u (2 Byte unsigned Value)
EIS 11u (4 Byte unsigned Value)
EIS 14u (1 Byte unsigned Value)
EIS 15 (14Byte Text)
Außerdem verfügt der Job über ein Freigabe Objekt, sowie über einen EIS 14 Ausgang für einen Error Code und einen EIS 15 Textausgang für einen Error Text. Sie werden ausgegeben, wenn die Checkbox bei „Laufzeitfehler ausgeben“ markiert ist.
Name
Pflichtfeld. Vergeben Sie einen eindeutigen Namen für den Job. Der Name darf maximal 15Zeichen enthalten.
Freigabeobjekt
Durch das Freigabeobjekt wird der Job freigegeben oder gesperrt. Es handelt sich um ein EIS 1 Objekt:
Gruppenadresse nicht vergeben = Job freigegeben
Gruppenadresse eingetragen, Wert 1 = Job freigegeben
Gruppenadresse eingetragen, Wert 0 = Job ist gesperrt
Gruppenadresse eingetragen, Kein Wert = Job ist gesperrt
Sobald eine Adresse in das Feld eingetragen ist, verhält sich die Freigabe entsprechend dem Wert der Gruppenadresse. Wurde auf die Adresse bisher kein Wert gesendet, ist sie also zurzeit Werte-los, ist der Job gesperrt.
Laufzeitfehler ausgeben
Ist dieses Flag aktiviert werden Fehlercodes per EIS 14 und Fehlertexte per EIS 15 Telegramm ausgegeben. Die Adressen dazu können in den Feldern darunter eingetragen werden. Eine Übersicht über die Fehlercodes befindet sich am Ende der Job Beschreibung.
Ausgang / Zugriff auf den Ausgangswert
Der Wert des Ausgangsobjekts kann mit Hilfe der Variablen „eo_out()“ auch für die Berechnung verwendet werden. Die Operation kann niemals durch „eo_out()“ angestoßen werden.
Eingänge
Pro Mathematik Job stehen 12 Eingangsobjekte zur Verfügung. Diese können den oben genannten Datentypen entsprechen. Außerdem kann bestimmt werden, wann ein Telegramm am ausgewählten Eingang die Berechnung der Formel anstößt. Die Gruppenadressen einzutragen, werden entweder über die Tastatur oder mittels des ESF-Dialoges eingetragen. Dabei drückt man die Pfeiltaste neben dem Adresseingabefeld und gelangt zur Übersicht über die Daten aus der ETS die man zuvor in den EIBPORT geladen hat (Siehe Kapitel KNXnet/IP | ETS).
Alle Werte innerhalb des Mathe Job werden grundsätzlich ‚unsigned‘ also ohne Vorzeichen berechnet. Sollen Werte mit Vorzeichen angezeigt werden, nehmen Sie bitte die entsprechenden Einstellungen im Visualisierungselement vor.
Berechnung der Formel
Die Auswahl im Dropdown Menü bestimmt, wann die Berechnung der Formel im Mathematischen Ausdruck angestoßen wird:
Immer: Die Berechnung wird angestoßen, sobald irgendein Eingang am Eingangsobjekt festgestellt wird.
Nie: Die Berechnung wird durch diesen Eingang niemals angestoßen. Natürlich wird der Wert des Eingangsobjektes bei der Ausführung der Operation berücksichtigt.
Bei Wertänderung: Nur wenn sich der Eingangswert gegenüber dem vorherigen Wert ändern, wird eine Berechnung angestoßen.
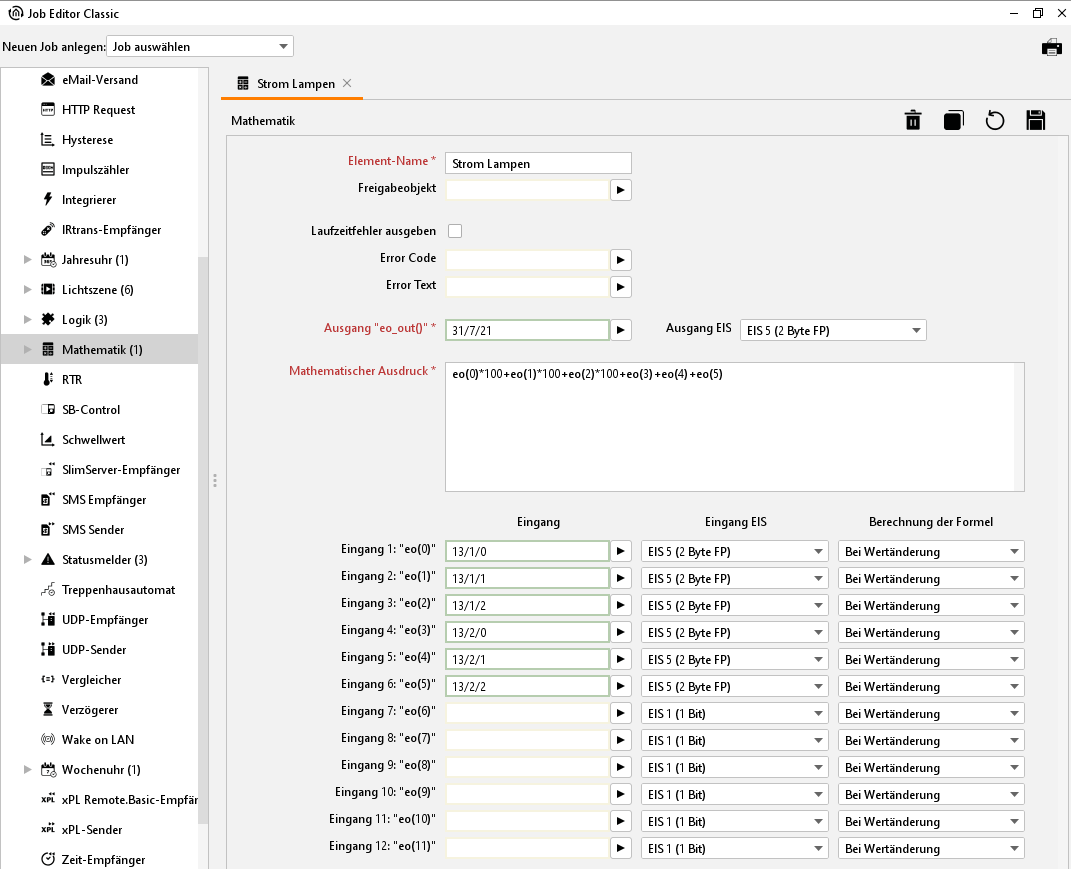
Job Editor Classic - Job Maske Mathematik
Zugriff auf die Eingänge im Mathematischen Ausdruck
Um die Werte der Eingangsobjekte für den mathematischen Ausdruck nutzen zu können gilt folgende Syntax:
Die Eingänge 1-12 haben die Index Nummern 0-11.
Durch die Eingabe von „eo([Indexnummer])“ wird der jeweilige Wert des Eingangsobjektes in den Mathematischen Ausdruck geholt. Für den Eingang 1 also „eo(0)“. Die jeweiligen Zeichenketten stehen auch in Anführungsstrichen hinter dem Eingangsnamen.
Soll umgekehrt der Index des Objektes ausgegeben (und evtl. weiterverwendet) werden auf dem zuletzt ein Telegramm eingegangen ist, so kann dies mit der Eingabe „eoi()“ geschehen.
Mathematischer Ausdruck
In diesem Feld wird der gewünschte mathematische Ausdruck zusammengesetzt. Dabei gelten die üblichen mathematischen Regeln. Bei Ausgabe des Ergebnisses ist es wichtig zu beachten, dass die Höhe des Ergebnisses nicht über den Werte Bereich des Datentyps vom Ausgangsobjekt hinausgeht! Folgende Operationen sind möglich:
Intern kann das Mathematik Modul nur mit Fließkommazahlen oder Texten arbeiten.
Mathematische Operationen:
Symbol | Beschreibung |
+ | Addition (bzw. Aneinanderreihung von Strings) |
- | Subtraktion |
* | Multiplikation |
/ | Division (reelwertig) |
% | Modulo (Rest nach einer ganzzahligen Division) |
& | bitweises "und“-ieren |
| | bitweises "oder“-ieren |
~ | bitweises negieren |
! | logisches negieren (NOT) |
^ | Potenzieren |
Logische (boolesche) Operationen
Symbol | Beschreibung |
|| | logisches ODER) |
&& | logisches UND |
> | Vergleichsoperation "Größer als" |
>= | Vergleichsoperation "Größer gleich" |
< | Vergleichsoperation "Kleiner als |
<= | Vergleichsoperation "Kleiner gleich |
== | Vergleichsoperation "Gleichheit |
Sonstige Operationen
Symbol | Beschreibung |
= | Zuweisung |
'(' und ')' | Klammerung zur Änderung des Operatorvorranges |
?: | If-Then-Else Operator |
Eingebaute Funktionen
Symbol | Beschreibung |
sqrt(x) | Quadratwurzelberechnung |
sin(x) | Sinusberechnung |
cos(x) | Cosinus Berechnung |
tan(x) | Tangensberechnung |
max(x,...) | Maximum Bestimmung von einer (endlichen) Menge von Werten |
min(x,...) | Minimumbestimmung von einer (endlichen) Menge von Werten |
rad(x) | Umrechnung Grad in Radianten (Bogenberechnung) |
asin(x) | Berechnung des Arkussinus |
acos(x) | Berechnung des Arkuskosinus |
atan(x) | Berechnung des Arkustangens |
ceil(x) | Berechnung des kleinsten ganzzahligen Wertes, der nicht kleiner als das Argument ist ("Aufrunden") |
floor(x) | Berechnung des größten ganzzahligen Wertes, der nicht größer als das Argument ist ("Abrunden") |
abs(x) | Berechnung des absoluten Wertes eines Arguments |
exp(x) | Berechnung der Exponentialfunktion zur Basis 'e' (Eulersche Konstante) |
log10(x) | Berechnung des 10er-Logarithmus |
pow(x,y) | Exponentialfunktion berechnet Oxyd |
time() | Liefert die Systemzeit in Sekunden seit dem Beginn der Epoche (00:00:00 UTC, January 1, 1970) |
srand(x) | Setzt den (Pseudo-)Zufallsgenerator auf einen definierten Startwert |
rand() | Liefert die nächste Zufallszahl |
eo_sum(x,...) | Addiert die EIB-Objekte mit den Nummern laut der Argumente auf |
int(x) | Schneidet die Real Zahl ab und liefert nur den ganzzahligen Wert zurück |
modf(x) | Liefert den Dezimalteil einer Real Zahl zurück (Die Stellen nach dem Komma) |
round(x) | Liefert eine korrekt gerundete Ganzzahl eines realen Argumentes |
eoiga() | Liefert die Gruppenadresse, welche die Berechnung ausgelöst hat (nicht formatiert!) |
eo_ga(idx, idx_ga) | Liefert die Gruppenadresse eines Objektes unformatiert. idx bestimmt die Indexnummer des Eingangs, idx_ga bestimmt die Indexnummer der Gruppenadresse im Objekt. Beides fängt bei „0“ an zu zählen (von links nach rechts). |
ga_str(ga, fmt) | Liefert die gewünschte Gruppenadresse (ga = Indexnummer) als String (EIS 15) auf den Ausgang. Mittels „fmt“ kann 2- oder 3-stellige Schreibweise bestimmt werden. |
str_ga(str) | Gibt eine gewünschte Gruppenadresse als Ganzzahl aus. 2- oder 3-stellige Schreibweise spielt keine Rolle. |
version() | Liefert die Versionsnummer des Mathematik Moduls zurück. Aktuell sind das „18“ = version 1.2 (0x12) und „17“ = version 1.1 (0x11). |
Zahlentypen/-arten und Strings:
Art | Schreibweise |
Integerzahlen | 42 |
Hexadezimalzahlen | 0x12ab |
Realzahlen | 1.23 (Dezimaltrennzeichen = „.“!) |
Exponentialzahlen | 1.23e3 für 1.23 * 10^3 oder 1023.0 |
Texte | "text" |
Als Dezimaltrennzeichen muss ein „.“ (Punkt) verwendet werden, andernfalls wird der Ausdruck ungültig.
Vordefinierte Konstanten:
Symbol | Beschreibung |
M_PI | Die Konstante Pi (3.14.....) |
M_E | Die Euler-Konstante (Basis des natürlichen Logarithmus) |
M_LOG2E | Logarithmus zur Basis 2 von 'e' |
M_LOG10E | Logarithmus zur Basis 10 von 'e' |
M_LN2 | Natürlicher Log. von 2 |
M_LN10 | Natürlicher Log. von 10 |
M_PI_2 | Pi dividiert durch 2 ("Pi-Halbe") |
M_PI_4 | Pi dividiert durch 4 ("Pi-Viertel") |
M_1_PI | Reziprok Wert von Pi (1 durch Pi) |
M_2_PI | 2 mal 1 durch PI |
M_2_SQRTPI | 2 mal 1 durch Wurzel Pi |
M_SQRT2 | Wurzel aus 2 |
M_SQRT1_2 | Der Kehrwert von Wurzel 2 (bzw. Wurzel aus 1/2) |
Selbst definierte Variablen und mehrere Ausdrücke nacheinander:
„a=10“ Weist der Variablen „a“ den Wert 10 zu. „a=1; b=2; a+b“ Weist den Variablen „a“ und „b“ die Werte 1 resp. 2 zu und liefert als Ergebnis „3“ zurück.
Auf diese Weise selbst definierte Variablen haben nur eine begrenzte Gültigkeit innerhalb einer Berechnung eines Ausdrucks!
Reservierte Variablen
Variable | Beschreibung |
override_addr | Wenn der Wert dieser Variable ungleich „0“ ist, wird die eigentliche Ausgangsadresse verworfen und stattdessen der Wert dieser Variablen als Ausgangsadresse interpretiert (1-stellige Schreibweise). |
override_eis | Wenn der Wert dieser Variablen ungleich „0“ ist, wird die eigentliche Datentypkonfiguration durch diese überschrieben. Dabei findet keine Anpassung des Wertes statt. |
override_skip_send | Ist der Wert dieser Variablen ungleich „0“ wird der Sendevorgang abgebrochen. Die laufende Berechnung führt zu keinem Ergebnis. |
override_keep_data | Ist der Wert dieser Variablen ungleich „0“ wird nicht der errechnete Ausgangswert, sondern der Eingangswert benutzt, der die Berechnung angestoßen hat. |
Beispiele:
Hier einige Beispiele damit die Benutzung der verschiedenen Funktionen und Operationen etwas klarer wird:
„eo(1) + 100“ -> Liefert den Wert des KNX-Objektes mit der Nummer 1 (im folgenden EO_1) plus 100 zurück. Wichtig ist immer die Beachtung des möglichen Wertebereiches des KNX-Ausgangs- Objektes!
„eo(3)*eo(4)“ -> Multipliziert EO_3 und EO_4. Wenn in einem Ausdruck EIB-Objekte verwendet werden, die im Editor nicht mit GA versehen sind, so wird ein Fehler gemeldet.
„100 / eo(1)“ -> Dividiert 100 durch EO_1. Achtung: Wenn auf den Eingang 1 eine Null gesendet wird, so liefert die Berechnung dieses Ausdrucks einen Laufzeitfehler! („Division durch Null“).
„sqrt(eo(0)^2+eo(1)^2)“ -> Berechnet die Länge der Hypotenuse in einem rechtwinkligen Dreieck, wenn auf EO_0 und EO_1 die Längen der Katheten gesendet werden. („Satz von Pythagoras“)
„eoi()“ -> Liefert eine 2, wenn auf dem KNX-Objekt mit der Nummer Zwei etwas empfangen wurde.
„eo(eoi())“ ->Liefert den empfangenen Wert zurück.
„eo(eoi())^2“ -> Berechnet das Quadrat für jeden empfangenen Telegramwert.
„rand()“ -> Gibt einen zufälligen Wert zurück.
„rand() & 0xff“ -> Begrenzt diesen Wert auf einen Wertebereich von 0 bis zu maximal 255. Damit wäre das Ergebnis in EIS_14 darstellbar.
„srand(time())“ -> Liefert nichts (bzw. Null) zurück, initialisiert aber den Zufallsgenerator mit einem pseudo-zufälligen Startwert.
„eo(0)+eo(2)+eo(3)+eo(1)+eo(5)+eo(6)+eo(4)“ -> Berechnet die Summe von mehreren KNX-Objekten.
„eo_sum(0,1,2,3,4,5,6)“ -> Wie oben, aber sehr viel „Laufzeit-freundlicher“ und einsichtiger.
„"foo" + "bar"“ -> liefert als Ergebnis „foobar“. Dieses kann dann aber nur als EIS 15 auf dem Ausgang ausgegeben werden.
„eo(0)>23?1:0“ -> Liefert eine 1 wenn der Wert des Eingangsobjekts über 23 (Grad EIS 5) liegt und eine 0 wenn der Wert kleiner oder gleich 23 ist.
„eo_ga(0,1)“ -> Liefert die 2. Gruppenadresse im ersten Eingangsobjekt (eo(0)) als unformatierte Zahl.
„ga_str(0,fmt==2)“ -> Liefert die Gruppenadresse des Eingangs 1 als String (EIS 15 Text) in 2-stelliger Schreibweise auf den Ausgang. fmt==3 liefert die Adresse 3-stellig.
„str_ga("17/1/2")“ -> Liefert die Zahl „35074“ auf den Ausgang.
„override_addr=(eo(0)>10?61482:61480); eo(0)>10?1:0“ -> sendet eine 1 auf die Adresse 30/0/42 wenn der Eingangswert eo(0) über 10 liegt, und eine 0 auf die Adresse 30/0/40 wenn der Eingangswert unter 10 liegt.
„override_addr=(eo(0)>10?61482:61480); override_eis=(eo(0)>10?1:9); eo(0)>10?1:2400“ -> sendet eine 1 als EIS 1 (1bit) auf die Adresse 30/0/42 wenn der Eingangswert eo(0) über 10 liegt, und sendet eine 2400 als EIS 9 (4byte) auf die Adresse 30/0/40 wenn der Eingangswert unter 10 liegt.
„override_skip_send=(eo(0)>10?1:0)“ -> Liegt der Eingangswert von eo(0) unter 10 wird eine 0 auf den Ausgang gesendet, wenn der Wert über 10 liegt sendet der Job keinen Ausgangswert.
„x=(eo(0)>10?1:0); override_keep_data=x“ -> Liefert einen Ausgangswert von 0 bis 10 oder den Wert des auslösenden Eingangstelegrams.
„version()“ -> Liefert bei einem beliebigen Eingangstelegram die aktuelle Versionsnummer des Mathejob als Zahl zurück.
Fehlercodes und Fehlertexte
Nummer | Bedeutung bzw. EIS 15 Textausgabe (in Englisch) |
0 | Kein Fehler |
42 | Syntaxfehler |
43 | Allgemeiner Laufzeitfehler (z.B. Division durch Null oder tan(PI/2)) |
1 | Fehlende rechte Klammer |
2 | Fehlende linke Klammer (bei eingebauter Funktion) |
3 | Fehlende rechte Klammer (stattdessen Ausdruck gefunden) |
4 | Unbekannte Variable |
5 | Unbekanntes Schlüsselwort |
6 | Fehler im Zeichenkettenausdruck: Z.k. kann keinen mathematischen Operator enthalten |
7 | Division durch Null |
8 | Z.k. kann nicht exponenziert werden |
9 | Fehler im Zeichenkettenausdruck: Z.k. kann nicht mit Operator vereinbart werden |
10 | Fehlende rechte Klammer oder Komma bei Funktionsaufruf |
11 | Fehlendes Komma |
12 | Fehlendes Argument |
50 | Fehler in EO-Funktion: Falsche Anzahl von Argumenten |
51 | Fehler in EO-Funktion: Falscher Index |
52 | Fehler in EO-Funktion: EO ist leer |
